Langsung ke konten utama

MASIH BERKUTAT DENGAN GEOGEBRA (SEGITIGA)

Kali ini membahas tentang :
1. Melukis Segitiga
2. Melukis Segitiga jika diketahui Dua Sisi dan Sudut Apit Kedua Sisi
3. Melukis Segitiga jika diketahui Satu Sisi dan Dua Sudut Pada Kedua Ujung Sisi
4. Melukis Garis Bagi dari Sebuah Segitiga
5. Melukis Garis Berat dari Sebuah Segitiga
6. Melukis Garis Sumbu dari Sebuah Segitiga
7. Melukis Garis Tinggi dari Sebuah Segitiga

Langsung saja membahasa ulasan yang pertama
Melukis Segitiga
1. Buatlah sebuah lingkaran A dengan jari-jari 4 menggunakan Center With Center and Radius

2. Letakkan kursor disembarang tempat dan akan muncul kolom untuk mengisi jari-jari lingkaran. Lalu isi jari-jari dengan angka 4 lalu OK dan akan muncul sebuah lingkaran


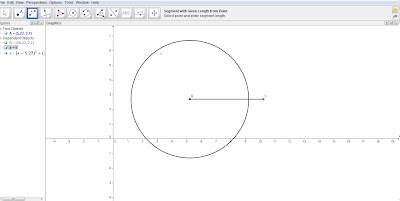
3. Buatlah garis dengan menggunakan Segment with Given Length From Point


4.  Klik kursor dititik pusat A dan akan muncul kolom untuk menentukan panjang garis. Isi Panjang Garis tersebut dengan angka 5 lalu OK sehingga terbentuklah garis AB 


5. Buatlah Lingkaran dititik pusat B menggunakan Circle With Center and Radius dengan jari-jari = 3

6. Klik Intersect Two Object, arahkan kursor ke Lingkaran dengan titik pusat A dan Lingkaran dengan titik pusat B untuk mengetahui titik perpotongan kedua lingkaran tersebut



Titik Perpotongannya yaitu Titik C dan Titik D


7. Klik Polygon untuk membuat Segitiga 

 8. Arahkan kursor ke Titik A -> B -> D -> A sehingga terbentuklah sebuah segitiga 
9. Klik Distance or Length untuk mengetahui panjang garis, arahkan kursor dari titik A -> B -> D -> A dengan otomatis akan muncul panjang garisnya

Komentar

Posting Komentar

Postingan populer dari blog ini

Gluten Free Pancake

Bismillahirrahmanirrahim Siapa yang disini sangat bahagia sekali kalau menemukan resep yang sesuai untuk masakan yang kita buat. Menemukan resep yang pas itu tidak cukup sekali percobaan saja tapi butuh berkali-kali uji coba. Entah adonan yang dibuat terlalu encer,  kurang air atau malah ketika semua adonannya sudah siap untuk diolah ternyata ketika memasaknya gosong haha ternyata masak tuh struggle sekali yah tetapi don't give up ya dan selalu optimis kalau masakan kita InsyaAllah bisa berhasil dan akhirnya dipuji puji sama suami, bonusnya bisa dikasih tambahan dana belanja 😁 Alhamdulillah. Nah kali ini aku akan berbagi resep menu andalanku kalau sudah bingung mau masak apa, tampilannya sederhana tetapi bisa mengenyangkan sekali ketika menyantapnya. Aku mau berbagi tentang resep pembuatan pancake , resep pancake yang aseli nya itu rata-rata menggunakan baking powder dan tepung terigu tetapi karena suami tidak bisa mengonsumsi pengembang dan tepung terigu aku menggantinya deng...
Posting Komentar
Baca selengkapnya

AWAL YANG BARU TENTANG MICROSOFT MATHEMATICS

Pengenalan Software Microsoft Mathematics Mean, Modus dan Median Langkah-langkah : 1. Buka Aplikasi Microsoft Mathematics 2. Pada kotak bergambar kalkulator gunakan Statistics, lalu masukkan fungsi Mean dan Insert Data Set. 3. Masukkan data-data sesuai yang diinginkan lalu OK dan Enter 4. Gunakan Langkah-langkah yang sama untuk mencari Modus dan Median Mean  Modus Median Menggunakan Microsoft Mathematics untuk Menentukan persamaan fungsi Integral Langkah-langkah : 1. Pada kotak bergambar kalkulator gunakan Calculus , lalu Input data dan Enter 2. Di Outpu t adalah hasil dari perhitungan Integral 3. Klik Graphing lalu Equation dan Function ,   copy persamaan fungsi Integral. 4. Paste Persamaan fungsi Integral dan Graph Membuat Parabola Langkah-langkah: 1. Klik Graphing lalu pada menu klik Equation & Functions 2. Insert data untuk menentukan persamaan Parabola yang berimpit di sumbu x positif 3. Kemudian Insert data untuk men...
Posting Komentar
Baca selengkapnya

NYAMAN ITU..........

     Setelah lulus kuliah hampir setengah tahun aku menjadi pengacara alias pengangguran banyak acara, terasa bosan hidupku yang tidak memiliki kegiatan yang tidak rutin meskipun ada pekerjaan sampingan tetap saja aku merasakan ‘hidup kok gini-gini aja’. Beberapa kali aku mencoba melamar di perusahaan dan institusi sekolah namun jawabannya semuanya sama ‘tunggu saja dulu yah’ aku menunggu dan terus menunggu mencoba bersabar, berdoa dan terus berikhtiar tapi tetap saja hati ini begitu gelisah, mulai merasakan ketidaknyamanan, dalam hatiku berkata ‘mau sampai kapan hidup membebani orangtua?. Alhamdulillah aku memiliki orangtua yang begitu bijak, terus menyemangati putrinya yang suka berkeluh kesah, mereka terus mengatakan ‘sabar nak, Allah sudah menyiapkan hal yang indah untukmu’ begitu tenang hati ini setiapkali mendengarkan nasihat yang begitu menyejukkan dari kedua orangtuaku. Beberapa hari kemudian ada seseorang dari bagian HRD yang memintaku untuk datang interview ke ...
8 komentar
Baca selengkapnya